Сегодня расскажем об одном из самых эффективных и широко применяемых на практике алгоритмов сортировки — быстрой сортировке, или Quick Sort, или qsort. Этот алгоритм был разработан более 40 лет назад, отчасти поэтому на практике в чистом виде он не встречается, так как уже есть способы добиться наибольшей эффективности при работе этого алгоритма.
Чтобы понимать, как и зачем этот алгоритм улучшается, нужно разобраться, как он работает в своём первозданном виде. Важно отметить, что для своей вычислительной эффективности этот алгоритм достаточно прост в понимании и реализации.
Алгоритм работает по принципу «разделяй и властвуй» — мы будем разделять массив и применять один и тот же алгоритм к его всё уменьшающимся частям. Общая схема алгоритма выглядит так:
- Из массива выбирается элемент, который называется pivot, т. е. опорный элемент.
- Далее запускается процедура разделения массива таким образом, чтобы в одной его части находились все элементы, которые меньше или равны опорному элементу, а во второй части — все элементы, которые больше опорного элемента.
- Для каждого подмассива, если в них больше двух элементов, рекурсивно запускается процедура, описанная в предыдущем пункте. Если элемента два, то они сравниваются друг с другом и при необходимости меняются местами.
После выполнения этих действий мы получим полностью отсортированный массив.
Рассмотрим подробнее второй пункт, что же там происходит. Для этого возьмём неотсортированный массив элементов [7, 2, 1, 8, 6, 3, 5, 4] и пройдёмся по шагам.
Шаг 1
Для начала выберем опорный элемент — возьмём последний элемент массива, он равен 4. Также введём два счётчика — i и j. Будем считать, что индексация в массиве начинается с 0. Тогда i = -1, а j = 0.
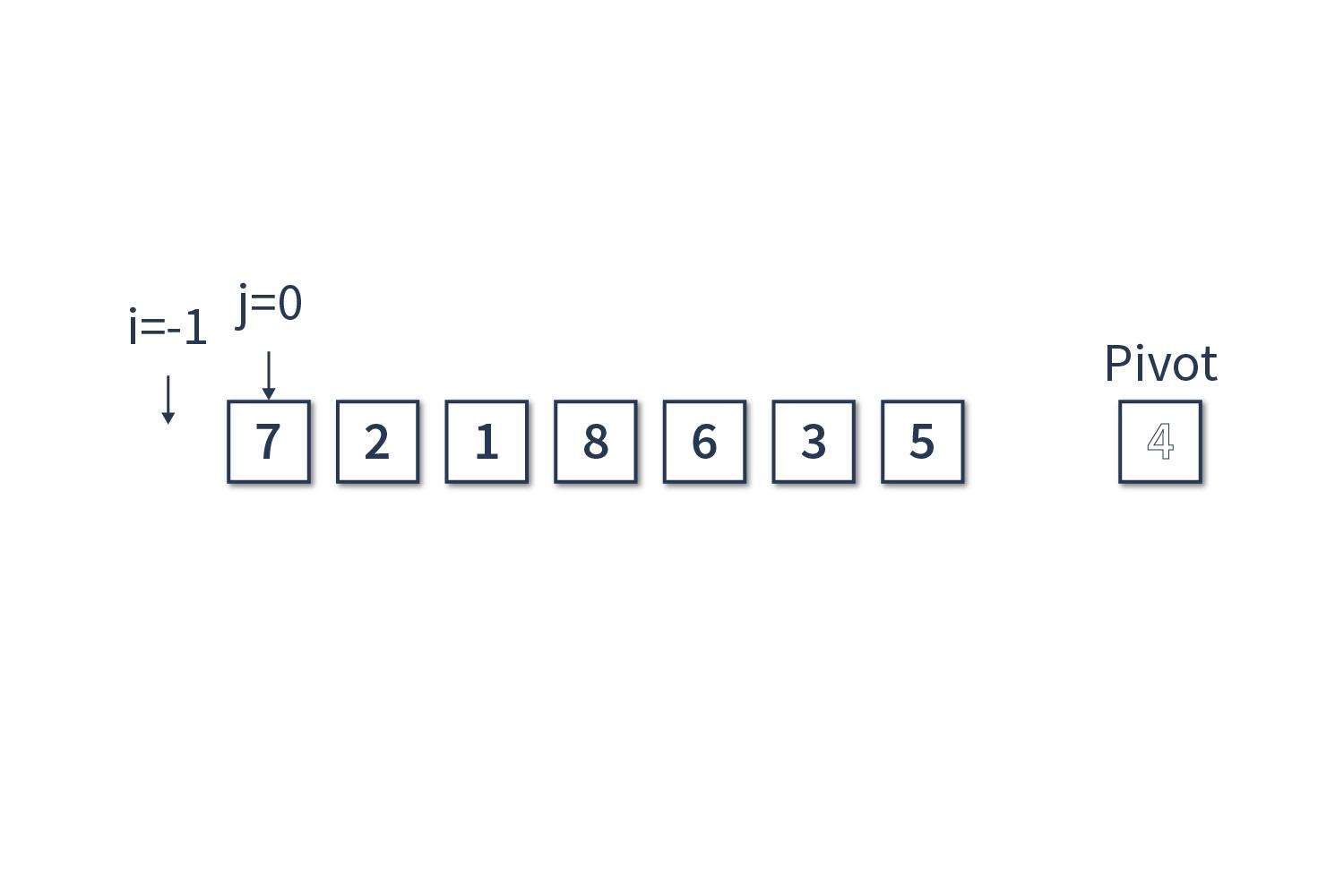
Сравниваем j-й элемент массива [7] с опорным элементом [4]. Если j-й элемент больше опорного, то просто инкрементируем счётчик j. В нашем случае на первом шаге мы так и сделаем.
Теперь j = 1, сравниваем j-й элемент массива [2] с опорным элементом [4]. Если он меньше опорного, то инкрементируем счётчик. Теперь i = 0, и меняем местами i-й и j-й элементы массива. В нашем случае меняем местами нулевой и первый элементы массива, получаем массив [2, 7, 1, 8, 6, 3, 5], опорный элемент [4] и инкрементируем счётчик j.
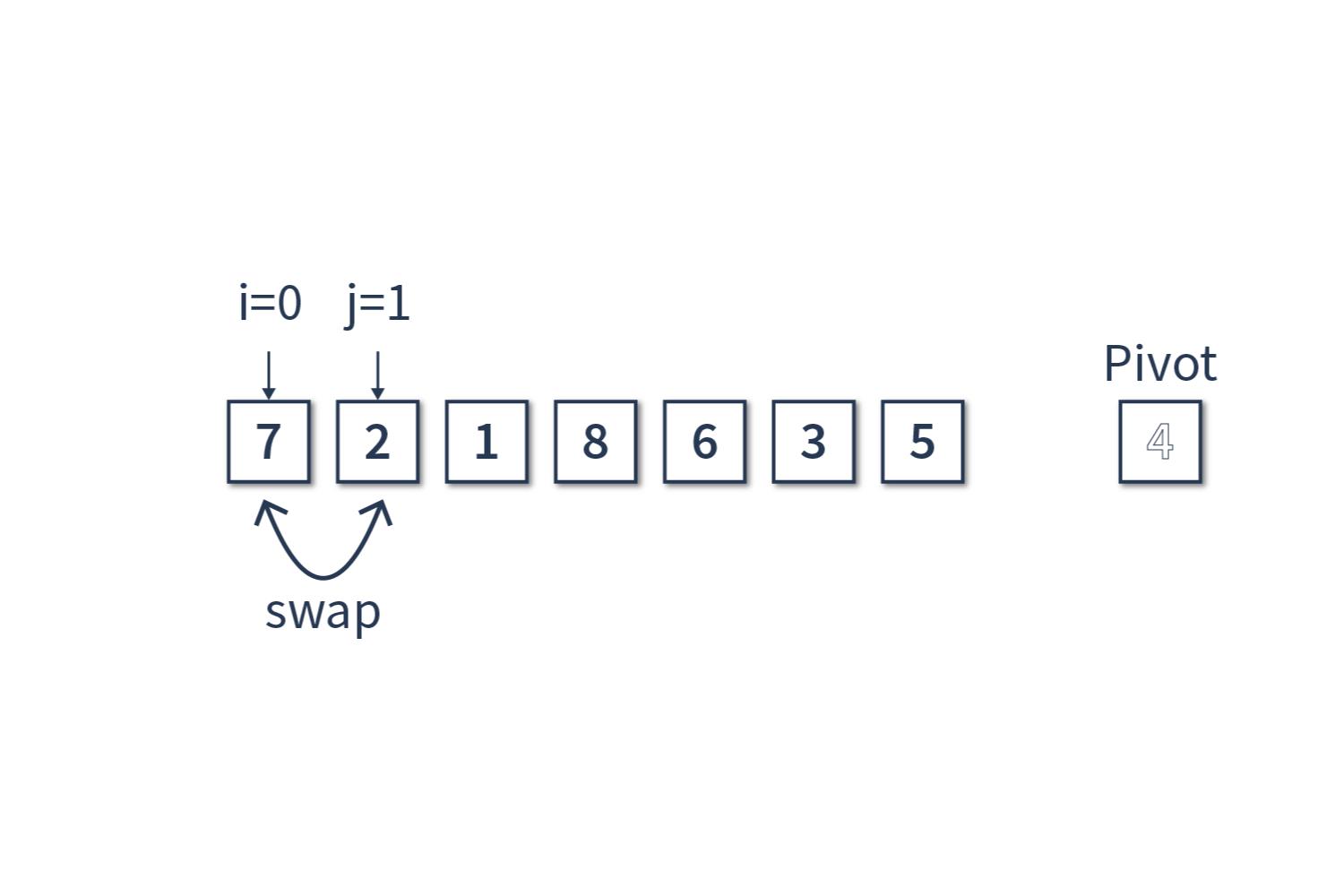
Далее шаг за шагом продвигаемся по массиву.
Шаг 2
Счетчик j = 2, сравниваем [1] и [4]. В этом случае инкрементируем i, i = 1 далее меняем местами i-й и j-й элементы массива [7] и [1], получаем массив [2, 1, 7, 8, 6, 3, 5], опорный элемент [4] и инкрементируем счётчик j.
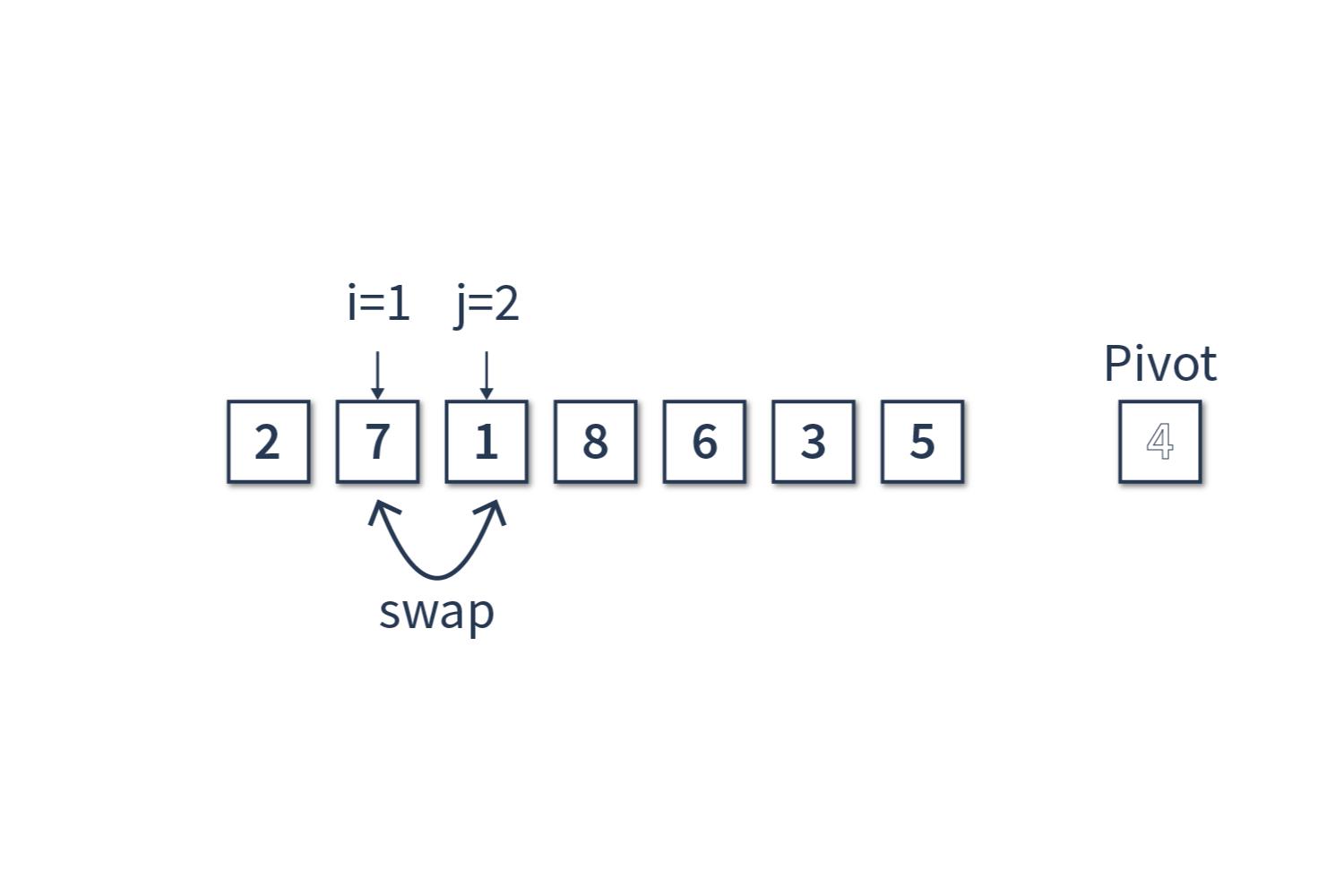
Шаг 3
Счетчик j = 3, сравниваем [8] и [4]. В этом случае инкрементируем только счётчик j.
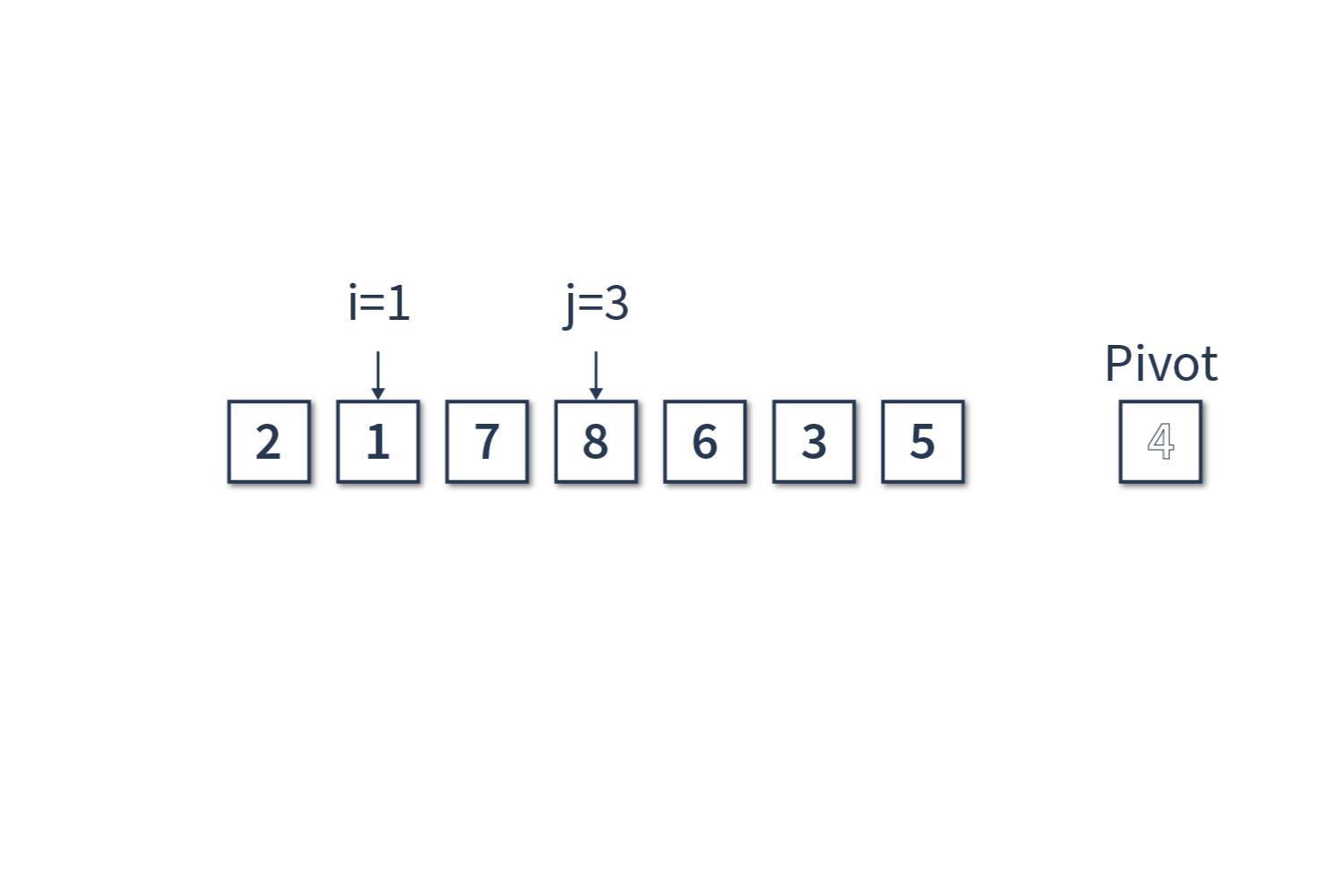
Шаг 4
Счётчик j = 4, сравниваем [6] и [4]. В этом случае инкрементируем только счётчик j.

Шаг 5
Счётчик j = 5, сравниваем [3] и [4]. В этом случае инкрементируем i, i = 2 и меняем местами i-й и j-й элементы массива [7] и [3], получаем массив [2, 1, 3, 8, 6, 7, 5], опорный элемент [4] и инкрементируем счётчик j.
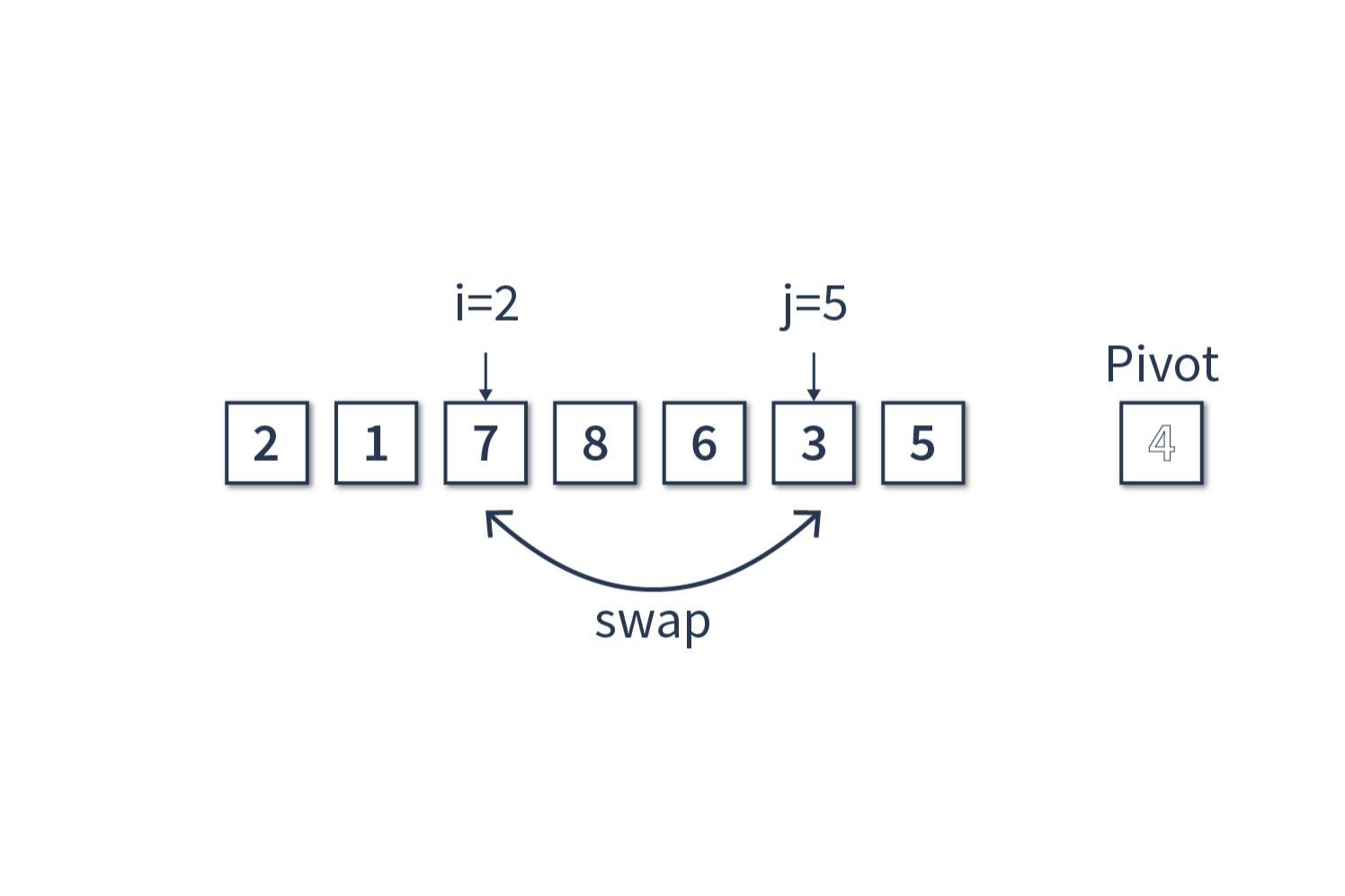
Шаг 6
Счётчик j = 6, сравниваем [5] и [4]. Счётчик j можно не инкрементировать, так как мы добрались до конца массива.
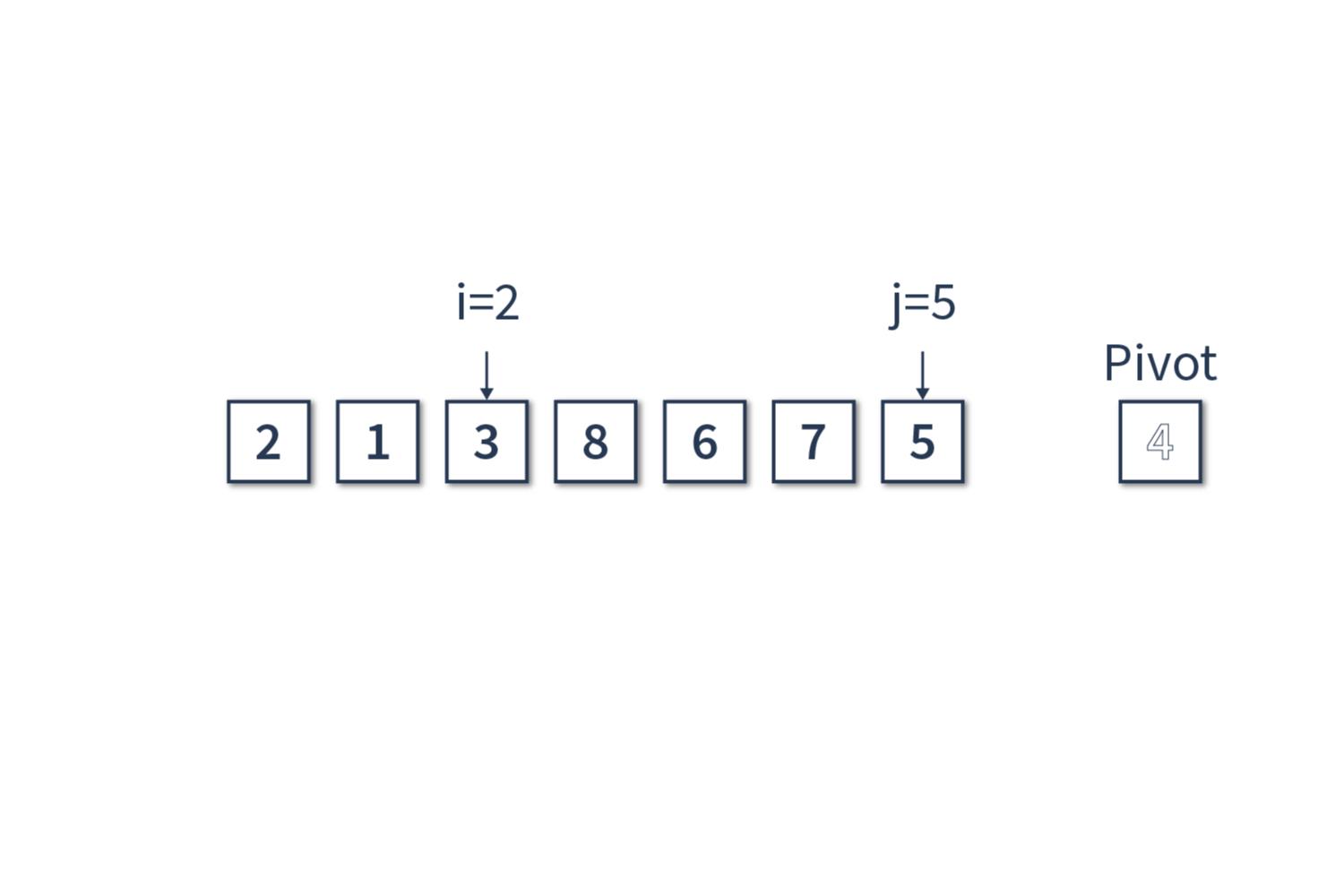
Теперь осталось найти местечко в массиве для нашего опорного элемента. Оно находится на i+1 позиции в массиве. Получаем [2, 1, 3] ≤ [4] < [8, 6, 7, 5]. Но так как подмассивы содержат более двух элементов, необходимо выполнить аналогичную сортировку для подмассива из элементов, которые меньше или равны опорному [2, 1, 3], и элементов, которые больше опорного [8, 6, 7, 5].
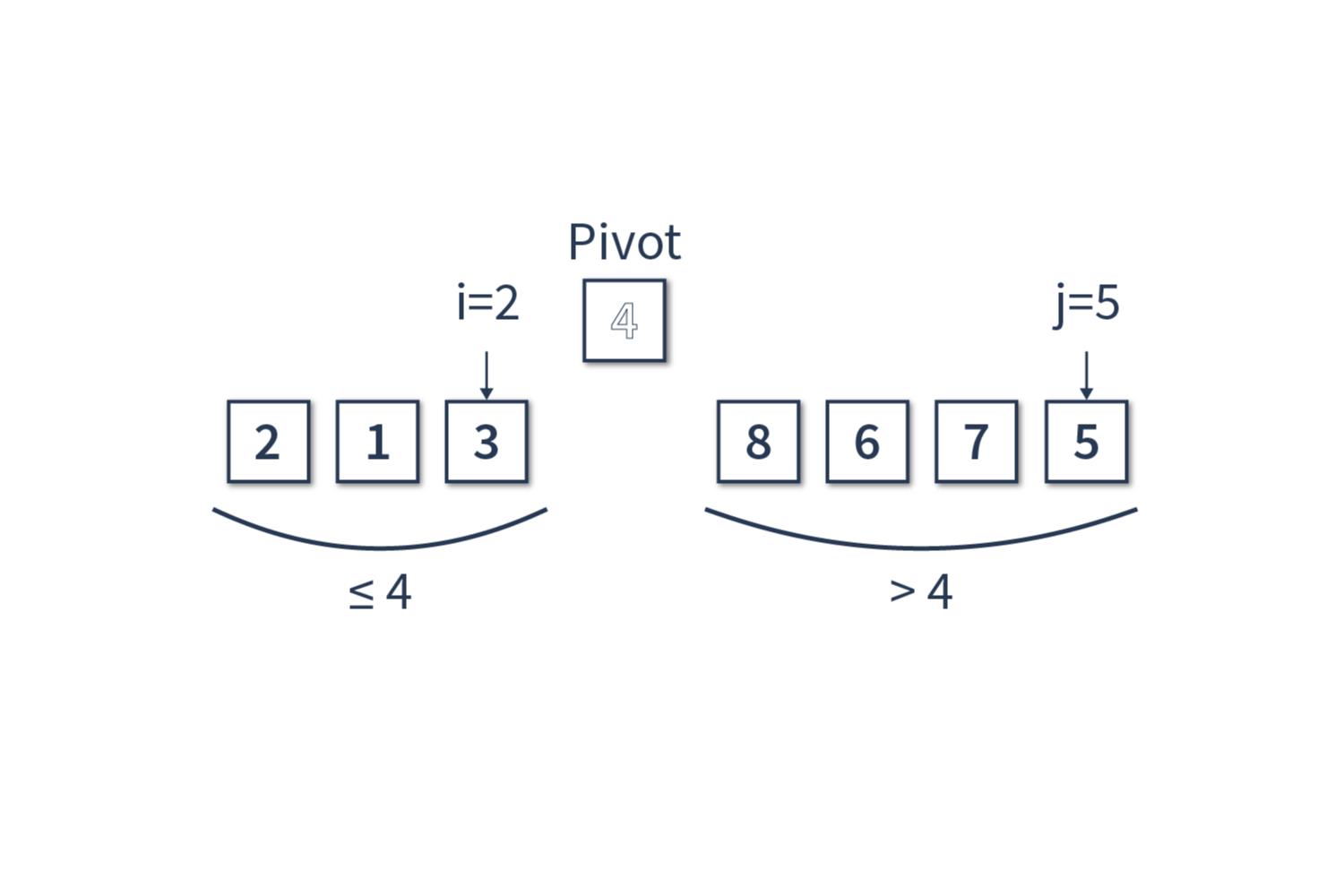
Далее вышеописанные действия повторяются для каждого из подмассивов до тех пор, пока массив не будет полностью отсортирован.
По этим шагам несложно реализовать алгоритм в коде.
Особенности алгоритма
Теперь поговорим о нюансах. Первый и вполне справедливый вопрос, почему мы выбрали опорный элемент именно так? Ответ прост: потому что так проще. Выбор опорного элемента — задача не из лёгких. То, насколько правильно он выбран, напрямую влияет на вычислительную сложность.
Пример выбора опорного элемента: взять первый, последний и средний элементы массива, отсортировать их и взять тот, что посередине. Таким простым действием можно улучшить качество выбранного опорного элемента.
Преимущества и недостатки алгоритма
Что касается сложности быстрой сортировки, то в лучшем случае мы получим сложность Ω (n log n), а в худшем — O(n2). Кроме низкой вычислительной сложности этот алгоритм обладает и другими достоинствами:
- на практике это один из самых быстродействующих алгоритмов внутренней сортировки;
- алгоритм довольно простой как для понимания, так и для реализации;
- требует лишь O(n) памяти, в случае улучшенной версии — O(1);
- допускает естественное распараллеливание для сортировки подмассивов;
- работает на связных списках;
- является наиболее эффективным для сортировки большого количества данных.
К недостаткам можно отнести:
- неустойчивость;
- вычислительная сложность сильно деградирует при неудачных входных данных.
Этот алгоритм, пусть и с модификациями, используется в различных языках программирования. Например, в Java его реализацию можно встретить в библиотеке java.util.Arrays, в методе sort(). А вот что написано в документации Oracle: “Реализация: в качестве алгоритма используется Dual-Pivot Quick Sort, разработанный Владимиром Ярославским, Джоном Бэнтли и Джошуа Блохом”. Поэтому этот алгоритм определённо достоин вашего внимания.
Ещё больше сортировок вы найдёте здесь:








